Ajándékozz éves hvg360 előfizetést!
Egy magát matematikai művészként jellemző szakember csodás rajzokat osztott meg a világgal, amelyek visszatérő körívekből állnak, méghozzá előre meghatározott képlet alapján.
Olvasóink 99,99999 százalékának vélhetően semmit sem mondana bármelyik képlete is, ezért inkább csak gyönyörködjünk abban, hogy Hamid Naderi Yeganeh matematikai művészetének szó szerint mi a végeredménye.
Persze aki kíváncsi rá, hogy a Huffington Postban megjelent, visszatérő körívekből álló képeknek milyen lehet a képlete, lejjebb görgetve a legalsó alkotásnak láthatja minden adatát.
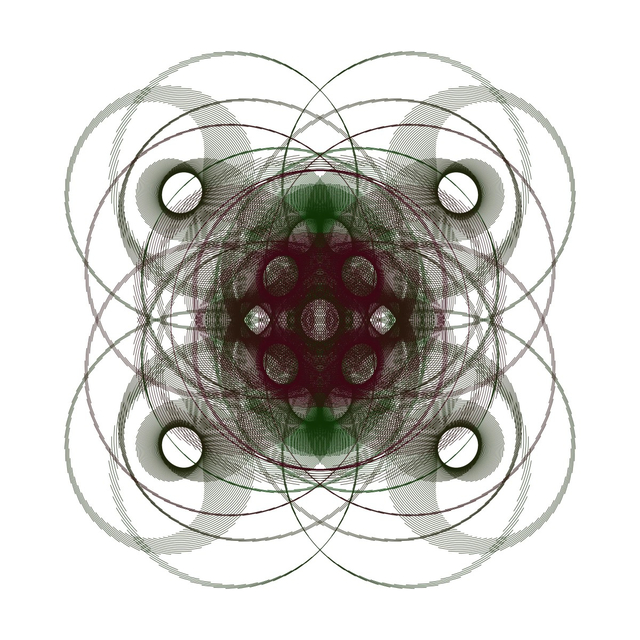
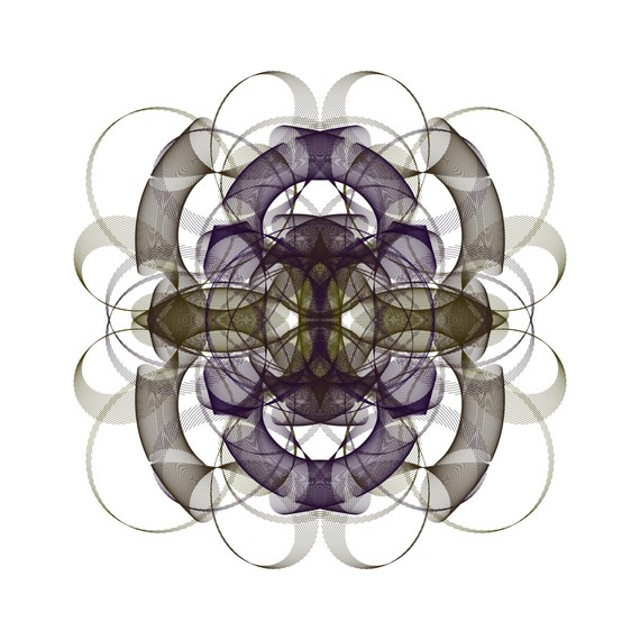
A legalsó képlete tehát a következő:
(S(k)cos(A(k))+X(k), S(k)sin(A(k))+Y(k)),
(S(k)cos(B(k))+X(k), S(k)sin(B(k))+Y(k)),
(S(k)cos(C(k))+X(k), S(k)sin(C(k))+Y(k)),
S(k)=(1/20)+(6/15)(sin(32πk/6000))2,
A(k)=(214πk/6000)+(π/20)+(19π/20)(sin(32πk/6000))4,
B(k)=(214πk/6000)-(π/20)-(19π/20)(sin(32πk/6000))4,
C(k)=(214πk/6000),
X(k)=(21/19)cos(18πk/6000)+(21/38)(cos(34πk/6000))3,
Y(k)=(21/19)sin(18πk/6000)+(21/38)(sin(58πk/6000))3.
