A feladat megoldásához a RÉSZLET (az angol nyelvű változatnál PMT)...
A feladat megoldásához a RÉSZLET (az angol nyelvű változatnál PMT) függvényt használjuk fel, amely kiszámítja állandó nagyságú törlesztőrészletek és kamatláb mellett a törlesztési időszakra vonatkozó tőke- és kamattörlesztési összeget (a költségek, adó nélkül).
Szintaxisa:
RÉSZLET(ráta; időszakok; mai_érték; jövő_érték; típus), ahol
ráta: Az időszakonkénti kamatláb, havi értéke =éves kamat%/12.
időszakok: A fizetési időszakok összes száma. Havi törlesztésnél év*12.
mai_érték: Jelenlegi érték, a jövőbeli kifizetések összegével egyenértékű egyösszegű
kifizetés. Ha nem adjuk meg, akkor a függvény 0 értéket tételez fel. Pozitív, ha felvesszük pénzt, negatív, ha kölcsönadunk.
jövő_érték: A jövőbeli érték vagy az utolsó részlet kifizetése után elérni kívánt összeg. Ha nem adjuk meg, akkor a program 0-nak tekinti (például egy kölcsön jövőbeli értéke 0). Ha például valamilyen célra 500000 Ft-ot szeretnénk megtakarítani 18 év alatt, akkor az 500000 Ft lesz a jövőbeli érték. Negatív értéke esetén, az időszak végén, a periodikus befizetéseken túl még fizetnünk kell, pozitív értéke esetén végül mi kapjuk meg ezt az összeget.
típus: Egész szám, a résztörlesztések esedékessége. 0 – fizetés az időszak végén (ez az alapértelmezett érték), 1 – fizetés az időszak kezdetén.
Írjuk be az =RÉSZLET(20%/12; 10; 1000000) képletet, amelynek eredménye:
–109394 Ft. Az éves törlesztés ennek 10-szerese (mert a törlesztési időszakok=10).

Nézzünk egy másik példát. Számítsuk ki egy 300000 Ft-os, 20,5%-os éves kamatrátájú, 72 hónap alatt visszafizetendő lakáskölcsön havi tőke- és kamattörlesztését minden év végén (az 1., 12., 24., 36., 48. és a 60. hónapban), ha mindig a hónap végén fizetünk.
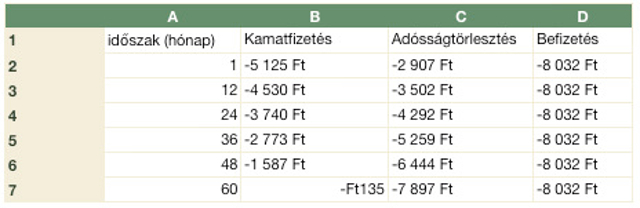
Ehhez készítsük el az alapadatok táblázatát, amelyben az A2:A7 tartomány tartalmazza az időszakok számát, azaz a kezdettől eltelt hónapokat, a B oszlopba kerülnek a kamatfizetések, a C oszlopba az adósság (tőke) törlesztés és a D oszlopba a havi befizetéseket írjuk. Alapadatként e három oszlopnak csak a nevét adjuk meg.
Írjuk a B2 cellába a kamatfizetés képletét: =RRÉSZLET(20,5%/12;A2; 60; 300000)
Írjuk a C2 cellába a tőketörlesztés képletét: =PRÉSZLET(20,5%/12; A2; 60; 300000)
Írjuk a D2 cellába a két megelőző cella összegét: =B2+C2
Jelöljük ki a B2:D2 cellákat, majd a tartomány kitöltőjelét húzzuk a D7 celláig. Az eredmény az ábrán látható. Megfigyelhetjük, hogy a törlesztést a kamatfizetéssel kezdjük, így adósságunk alig csökken.
Nincs még vége persze. Kicsit bonyolítsuk tovább a dolgokat. Számítsuk ki egy 300000 Ft-os, 20,5%-os éves kamatrátájú, 72 hónap alatt visszafizetendő lakáskölcsön évenként visszafizetendő kamattörlesztését minden év végén (az 1., 12., 24., 36., 48. és a 60. hónapban). Szép feladat!
A megoldás: a kamattörlesztések halmozott összegének kiszámítására a CUMIPMT függvényt használjuk.
Szintaxisa: CUMIPMT(ráta; időszakok; mai_érték; kezdő_p; vég_p; típus), ahol a RÉSZLET függvény argumentumain túl:
kezdő_p: Az első törlesztési időszak. Az időszakok számozása 1-gyel kezdődik.
vég_p: Az utolsó törlesztési időszak (vég_p>kezdő_p).
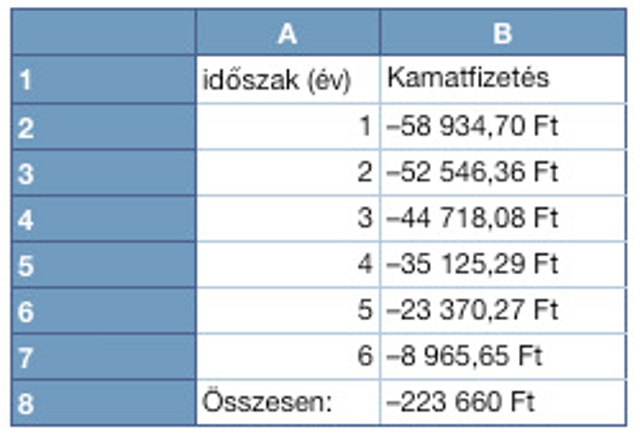
Írjuk be az A2:A7 cellákba a vizsgált éveket.
Írjuk be a B2 cellába az =CUMIPMT(20,5%/12; 72; 300000; (A2-1)*12+1; A2*12; 0), képletet.
A B2 cella kitöltőjelét egérrel húzzuk a B7 celláig.
Az eredmény az ábrán látható. Megfigyelhető, hogy a hat év alatt összesen 223660 Ft kamatot fizetünk vissza.
Végül egy utolsó próba, hogy kellően begyakoroljuk az Excel ezirányú használatát: Számítsuk ki egy 300000 Ft-os, 20,5%-os éves kamatrátájú, 72 hónap alatt visszafizetendő lakáskölcsön évenként visszafizetendő tőketörlesztését minden év végén (az 1., 12., 24., 36., 48. és a 60. hónapban).
A megoldás immár egyszerűnek tűnhet:
A kamattörlesztések halmozott összegének kiszámítására a CUMPRINC függvényt használjuk.
Szintaxisa: CUMPRINC(ráta; időszakok; mai_érték; kezdő_p; vég_p; típus), ahol az argumentumok megegyeznek a fentebb tárgyaltakkal.
Írjuk be a B2 cellába az =CUMPRINC(20,5%/12; 72; 300000; (A2-1)*12+1; A2*12; 0), képletet.
A B2 cella kitöltőjelét egérrel húzzuk a B7 celláig.
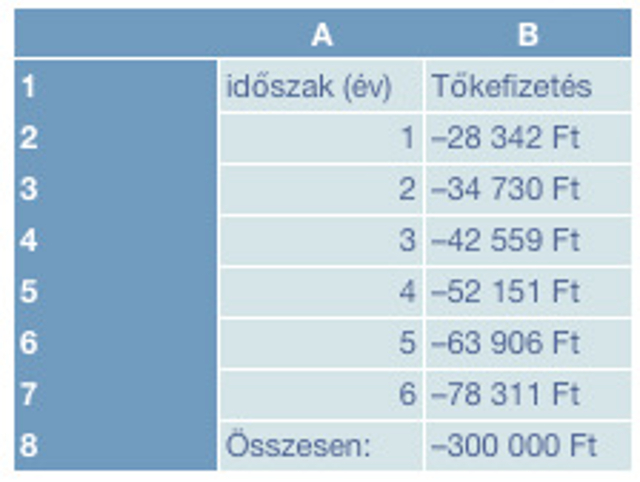
Az eredmény az ábrán látható. Megfigyelhetjük, hogy a törlesztési időszak végére a teljes tőkét visszafizetjük.


 Ajándékozz éves hvg360 előfizetést!
Ajándékozz éves hvg360 előfizetést!













