Ajándékozz éves hvg360 előfizetést!
Bár Vekerdy tanár úr is megmondta, hogy a gyerekkel együtt tanulni semmi jóra nem vezet, a jelenlegi helyzet felülírja ezt a szabályt. Próbáljunk meg hát csak a jóra emlékezni, és idézzük fel a rég tanultakat. Gyorstalpalónkon - amelyhez a Segíts a gyerekednek! Matek lépésről lépésre és a Hogyan legyünk jók matekból? című könyveinket vetettük be - három matematikai anyaghoz adunk rövid leírást.
Felértékelődnek a matekhoz értő családtagok, és a szülői korrepetálás reneszánszát éli. Itt az ideje, hogy elővegyük a matekkönyvet − mi is így tettünk. Nem reprezentantív, szűk körű igényfelmérésünk eredményeképpen a Pitagorasz-tétel és a négyszögek fajtáinak vizuális magyarázata, valamint a három alapvető számolási szabály került bele felvilágosító összeállításunkba.
Mi az a Pitagorasz-tétel?
A Pitagorasz-tétel kimondja, hogy a derékszögű háromszög két befogójának hosszát a négyzetre emelve és összeadva megkapjuk a leghosszabb oldal négyzetét. A „négyzetre emelés” kifejezés szó szerint is értelmezhető, mintha valóban három négyzettel lenne dolgunk. Az ábrán látható, hogy az oldalakra helyezett, „emelt” három négyzet közül a legnagyobb területe megegyezik a két másik négyzet területének összegével.
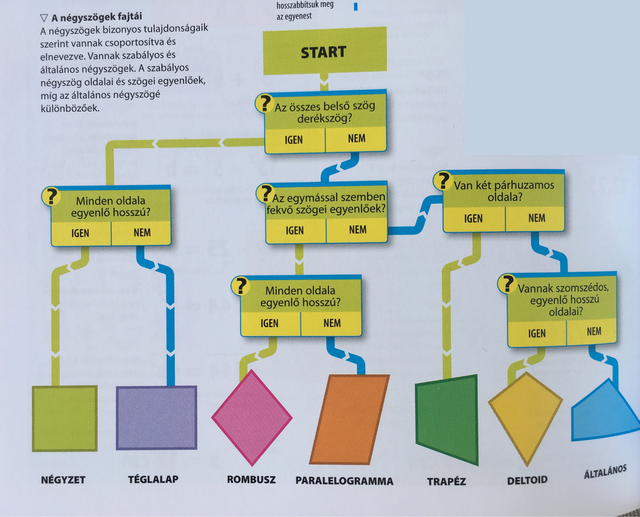
A négyszögek fajtái, jellemzőik
A négyszög kétdimenziós alakzat, amelyet négy szakasz határol. Négy csúcsa van (az oldalak találkozási pontjai) és négy belső szöge. A négyszögek belső szögeinek összege mindig 360°. A külső szög és a hozzá tartozó belső szög összege mindig 180°, mivel egyenesszöget alkotnak.
Többféle négyszög létezik, melyek tulajdonságai eltérőek. Ha az egyik csúcsból a szemközti csúcsba egy átlót húzunk, az a négyszöget két háromszögre osztja. Mivel a háromszög szögeinek összege 180°, így a négyszög belső szögeinek összege 2 × 180°.
A négyszögeket bizonyos tulajdonságaik szerint csoportosíhatjuk, az alábbi ábra segít ezt átlátni és memorizálni.
Számolási szabályok
Amikor számolunk, fontos emlékezni a következő három alapvető szabályra:
A kommutatív szabály: Amikor két számot összeadunk vagy szorzunk, nem számít, milyen sorrendben csináljuk – az eredmény mindig ugyanaz lesz.
Az asszociatív szabály: Amikor három vagy több számot adunk össze vagy szorzunk, nem befolyásolja az eredményt a számok csoportosítása. Az asszociatív szabály segítségével nagy számokat is könnyebben össze tudunk adni. Vegyük például ezt a műveletet: 136+47. Ha a 47-et felbontjuk így: 40 + 7, könnyebb lesz dolgozni a számokkal. 136+40+7= 183.
A disztributív szabály: Ha egy számot megszorzunk néhány szám összegével, ugyanazt az eredményt kapjuk, mint ha a számokat külön-külön szorozzuk meg. Lássuk, hogyan segít a disztributív szabály a 3 × 14 kiszámolásában. Ez elég nehéz feladat, ha nem tudjuk a 3-as szorzótáblát 14-ig, ezért inkább bontsuk fel a 14-et 10 + 4-re, így egyszerűbb lesz számolni. Ezután a művelet elvégzését egyszerűsíthetjük azzal, hogy a 3-at a zárójelben szereplő mindkét számmal megszorozzuk. Oldjuk meg a két zárójelben lévő műveletet, mielőtt összeadnánk őket: (3 × 10) + (3 × 4) = 30 + 12 = 42. Tehát azzal, hogy a 14-et egyszerűbb számokra bontottuk, és mindkettőt 3-mal szoroztuk, megkaptuk, hogy 3 × 14 = 42.
Semmelweis nagy felfedezése: milyen kapcsolat volt a gyermekágyi láz és a kézmosás között?
